Выбираем метод поиска по базе данных
Поиск – это нахождение какой-либо конкретной информации в большом объеме ранее собранных данных. Данные делятся на записи, и каждая запись имеет хотя бы один ключ. Ключ используется для того, чтобы отличить одну запись от другой. Записи, или элементы списка, идут в массиве последовательно и между ними нет промежутков. Целью поиска является нахождение всех записей подходящих к заданному ключу поиска.
Суть различных методов поиска сосредоточена в методах перебора, в стратегии поиска. Возникает ряд вопросов, ответы на которые зависят от структуры данных, в которой хранится множество элементов. Накладывая ограничения на структуру исходных данных, можно получить множество разнообразных стратегий поиска различной степени эффективности.
Последовательный поиск. Суть метода – последовательно перебираются все элементы массива, если на каком-то шаге цикла обнаруживается, что массив закончился или обнаруживается искомый элемент, то цикл заканчивается. Перед алгоритмом поиска стоит задача определения расположения ключа, потому он возвращает индекс записи, содержащей нужный ключ. Если ключевое значение не найдено, когда поиск завершился, то алгоритм поиска обычно возвращает значение индекса, которое превышает верхнюю границу массива.
У алгоритма последовательного поиска есть два недостатка или затруднительных случая. В первом случае целевой элемент стоит в списке последним. Во втором его вовсе нет в списке. В обоих случаях алгоритм выполнит n сравнений, где n – число элементов в списке.
Возможно проанализировать средний случай данного алгоритма. Для алгоритмов поиска возможны два средних случая. В первом предполагается, что поиск всегда завершается успешно, во втором — что иногда целевое значение в списке отсутствует. Целевое значение, если оно содержится в списке, может занимать одно из N возможных положений: первое, второе и т.п. Предположим, что все эти положения равновероятны (вероятность встретить каждое 1/n). Тогда, для каждого из N случаев число сравнений совпадает с номером искомого элемента. Получаем равенство
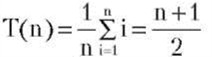
Целевое значение может не содержаться в списке. В результате число возможностей возрастет до n + 1 (если же элемент отсутствует в списке. то его поиск требует n сравнений). Предположим, что все эти положения равновероятны
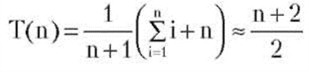
Возможность отсутствия элемента в списке увеличивает сложность среднего случая лишь на 1/2, хотя эта величина пренебрежимо мала по сравнению с длиной списка, которая может быть очень велика.
Если вероятность встретить искомый элемент в списке равна
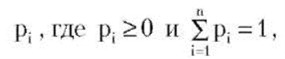
то средняя сложность поиска элемента равна 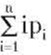 Рассмотрим закон Зипфа:
Рассмотрим закон Зипфа: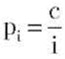 для i = 1,2,…,n с нормирующей константой
для i = 1,2,…,n с нормирующей константой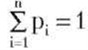
Допустим, что элементы массива А упорядочены согласно указанным частотам, тогда получим и среднее время успешного поиска составит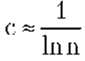
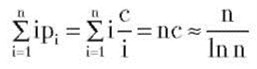
что меньше (n+1)/2. Исходя из этого можно сказать, что даже простой последовательный поиск требует выбора разумной структуры данных множества для более эффективной работы алгоритма.
Сложность алгоритма линейна – O(n).
Двоичный (бинарный или метод делением пополам). Суть метода в следующем: сначала производится проверка среднего элемента. Если его ключ равен ключу требуемого элемента, то поиск завершен. Если его ключ больше ключа требуемого элемента, то поиск необходимо продолжить в левой части массива. В противном случае поиск необходимо продолжить в правой части массива. Этот процесс повторяется до тех пор, пока не будет найден требуемый элемент или не будет больше элементов для проверки.
У алгоритма бинарного поиска есть определенный затруднительный случай. Так как алгоритм всякий раз делит список пополам, можно предположить, что n = 2k-1 для k. На некотором проходе цикл имеет дело со списком из 2j-1 элементов. При j = 1 производится
последняя итерация цикла, когда размер оставшейся части становится равным единице. Можно сделать вывод, что количество проходов не превышает k при n = 2k-1. Таким образом, в наихудшем случае количество проходов – k = log2(n+1).
Следовательно, алгоритм двоичного поиска имеет сложность по времени O(log2n), где n – число элементов отсортированного массива.
Метод двоичного поиска предназначен для сортированных элементов на смежной памяти фиксированного размера. Таким образом, если размерность вектора динамически изменяется, то экономия от использования двоичного поиска не компенсирует затрат на поддержание упорядоченного расположения al < a2 < … < an.
Выводы – выбор метода поиска. Выбор того или другого метода поиска зависит от определенных условий.
Если массив является неупорядоченным, то единственный алгоритм поиска, применимый в этом случае – последовательный. Этот метод применим для неупорядоченной информации, но также можно использовать его и на отсортированных данных. Когда данных немного, последовательный поиск работает достаточно быстро. Но если информация хранится на диске, поиск может занимать продолжительное время. Последовательный поиск достаточно прост и его легко запрограммировать, но время его работы прямо пропорционально количеству данных, которые нужно просмотреть; удвоение количества элементов приведет к удвоению времени на поиск, если искомого элемента в массиве нет. Это линейное соотношение (время выполнения является линейной функцией от размера данных), поэтому такой метод также называется линейным поиском. Потому эффективность этого метода очень низкая, так как для отыскания одного элемента в массиве размерности N в среднем нужно сделать N/2 сравнений. В лучшем случае он проверяет только один элемент, а в худшем — n.
Кроме поиска иногда нужно вставлять и удалять элементы. Однако массив плохо приспособлен для выполнения этих операций.
Приведенная ниже функция производит поиск в массиве символов известной длины, пока не найдет элемент с заданным ключом:

В данном случае items — это указатель на массив, который содержит информацию. Функция возвращает индекс подходящего элемента, если такой существует, либо -1, если такового нет.
Однако если данные уже отсортированы, можно применить двоичный поиск, который находит данные быстрее. Алгоритм двоичного поиска является систематизированной версией поиска слова в словаре. Для массива большого объема более эффективно было бы использовать двоичный поиск. Недостаток бинарного поиска заключается в необходимости последовательного хранения списка, что усложняет операции добавления и исключения элементов.
Рассмотрим функцию двоичного поиска для массивов символов в виде примера. Поиск возможно адаптировать для произвольных структур данных, если изменить фрагмент сравнения.
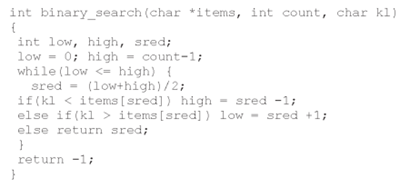
Двоичный поиск отбрасывает за каждый шаг половину данных, поэтому количество шагов пропорционально тому, сколько раз мы можем поделить n на 2, пока у нас не останется один элемент. Без учета округления это число равно log2 n. Если у нас в массиве 1000 элементов, то линейный поиск займет до 1000 шагов, в то время как двоичный — только около 10; при миллионе элементов линейный поиск займет миллион шагов, а двоичный — 20. Очевидно, чем больше число элементов, тем больше преимущество двоичного поиска, который работает быстрее, чем линейный.